Omo dėsnis visai grandinei ir grandinės atkarpai: formulės rašymo, aprašymo ir paaiškinimo parinktys

Profesionalus elektrikas ar elektronikos specialistas jokiu būdu negali apeiti Ohmo įstatymo savo veikloje, spręsdamas bet kokias problemas, susijusias su elektroninių ir elektros grandinių nustatymu, reguliavimu ir taisymu.

Tiesą sakant, kiekvienas turi suprasti šį įstatymą. Nes su elektra kasdieniniame gyvenime tenka susidurti kiekvienam.

Ir nors vokiečių fiziko Ohmo dėsnis yra numatytas vidurinės mokyklos mokymo programoje, praktiškai jis ne visada išmokamas laiku. Todėl savo medžiagoje apsvarstysime tokią aktualią gyvenimo temą ir suprasime formulės rašymo galimybes.

Viena sekcija ir visa elektros grandinė

Atsižvelgiant į elektros grandinę Omo dėsnio taikymo grandinei požiūriu, reikėtų atkreipti dėmesį į du galimus skaičiavimo variantus: atskiram skyriui ir visavertei grandinei.

Elektros grandinės sekcijos srovės apskaičiavimas

Elektros grandinės atkarpa, kaip taisyklė, laikoma ta grandinės dalimi, kuri pašalina EML šaltinį, nes turi papildomą vidinę varžą.

Todėl skaičiavimo formulė šiuo atveju atrodo paprasta:

I = U/R,

Kur atitinkamai:

• aš – srovės stiprumas;
• U – taikoma įtampa;
• R - pasipriešinimas.

Formulės aiškinimas paprastas – tam tikra grandinės atkarpa tekanti srovė yra proporcinga jai taikomai įtampai, o varža atvirkščiai proporcinga.

Vadinamoji grafinė „ramunė“, per kurią pateikiamas visas Omo dėsniu pagrįstų formuluočių variantų rinkinys. Patogus įrankis saugojimui kišenėje: sektorius "P" - galios formulės; sektorius „U“ - įtampos formulės; sektorius „I“ - dabartinės formulės; sektorius „R“ - pasipriešinimo formulės

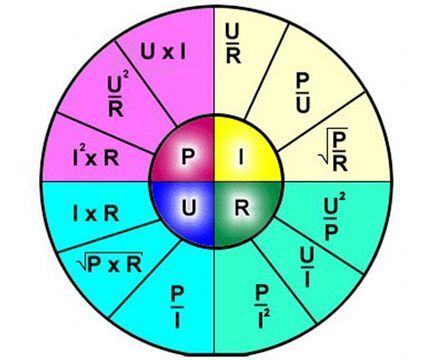
Taigi formulė aiškiai apibūdina srovės srauto per atskirą elektros grandinės sekciją priklausomybę nuo tam tikrų įtampos ir varžos verčių.

Formulę patogu naudoti, pavyzdžiui, skaičiuojant varžos, kurią reikia įlituoti į grandinę, parametrus, jei nurodyta įtampa ir srovė.

Omo dėsnis ir dvi pasekmės, kurias turi žinoti kiekvienas profesionalus elektromechanikas, elektros inžinierius, elektronikos inžinierius ir visi, susiję su elektros grandinių veikimu. Iš kairės į dešinę: 1 - srovės nustatymas; 2 - atsparumo nustatymas; 3 - įtampos apibrėžimas, kur I - srovė, U - įtampa, R - varža

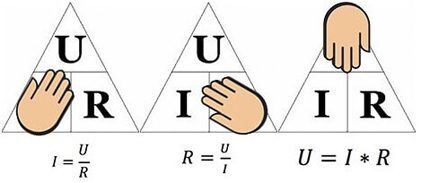
Aukščiau pateiktas paveikslas padės nustatyti, pavyzdžiui, srovę, tekančią per 10 omų varžą, kuriai taikoma 12 voltų įtampa. Pakeitę reikšmes, randame – I = 12 / 10 = 1,2 ampero.

Panašiai sprendžiamos varžos (kai srovė ir įtampa) arba įtampos (kai įtampa ir srovė žinomos) radimo problemos.

Taigi visada galite pasirinkti reikiamą darbinę įtampą, reikiamą srovės stiprumą ir optimalų varžinį elementą.

Siūloma naudoti formulė nereikalauja atsižvelgti į įtampos šaltinio parametrus.Tačiau grandinė, kurioje yra, pavyzdžiui, baterija, bus apskaičiuojama naudojant kitą formulę. Diagramoje: A – ampermetro įjungimas; V – įjungti voltmetrą.

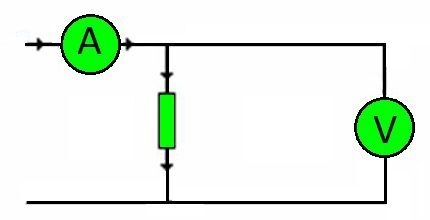
Beje, bet kurios grandinės jungiamieji laidai yra varžos. Apkrovos dydis, kurį jie turi atlaikyti, nustatomas pagal įtampą.

Atitinkamai, vėlgi naudojant Ohmo dėsnį, tampa įmanoma tiksliai pasirinkti reikiamą laidininko skerspjūvį, priklausomai nuo šerdies medžiagos.

Mūsų svetainėje yra išsamios instrukcijos kabelio skerspjūvio skaičiavimas pagal galią ir srovę.

Skaičiavimo parinktis visai grandinei

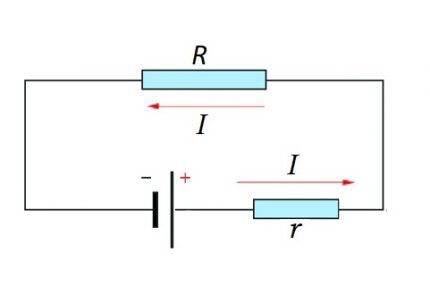
Visą grandinę sudaro dalis (sekcijos), taip pat EML šaltinis. Tai yra, iš tikrųjų EMF šaltinio vidinė varža pridedama prie esamos grandinės sekcijos varžinio komponento.

Todėl logiška šiek tiek pakeisti aukščiau pateiktą formulę:

I = U / (R + r)

Žinoma, EML vidinės varžos vertė pagal Ohmo dėsnį visai elektros grandinei gali būti laikoma nereikšminga, nors ši varžos vertė labai priklauso nuo EML šaltinio struktūros.

Tačiau skaičiuojant sudėtingas elektronines grandines, elektros grandines su daugybe laidininkų, svarbus veiksnys yra papildomos varžos buvimas.

Atliekant skaičiavimus visos elektros grandinės sąlygomis, visada atsižvelgiama į EML šaltinio varžą. Ši vertė sumuojama su pačios elektros grandinės varža. Diagramoje: I - srovės srautas; R — išorinis varžinis elementas; r yra EML (energijos šaltinio) varžos koeficientas.

Tiek grandinės atkarpai, tiek visai grandinei reikia atsižvelgti į natūralų momentą - nuolatinės arba kintamos srovės naudojimą.

Jei aukščiau paminėti punktai, būdingi Omo dėsniui, būtų vertinami nuolatinės srovės naudojimo požiūriu, atitinkamai su kintamąja srove viskas atrodo kiek kitaip.

Įstatymo poveikio kintamajam dydžiui svarstymas

„Atsparumo“ kintamosios srovės sąlygoms sąvoka turėtų būti labiau panaši į „impedanso“ sąvoką. Tai reiškia varžinės apkrovos (Ra) ir reaktyviosios rezistoriaus apkrovos (Rr) derinį.

Tokius reiškinius sukelia indukcinių elementų parametrai ir perjungimo dėsniai, susiję su kintamos įtampos verte – sinusine srovės reikšme.

Tai yra lygiavertė kintamosios srovės elektros grandinės grandinė, skirta apskaičiuoti naudojant formules, pagrįstas Omo dėsnio principais: R - varžinis komponentas; C yra talpinis komponentas; L – indukcinis komponentas; EML yra energijos šaltinis; I - srovės srautas

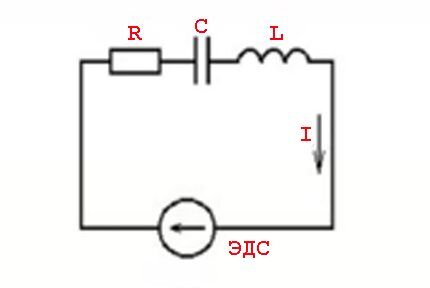
Kitaip tariant, nuo įtampos verčių atsiranda srovės verčių įtaka (atsilikimas), kurią lydi aktyviosios (varžinės) ir reaktyviosios (indukcinės arba talpinės) galios atsiradimas.

Tokie reiškiniai apskaičiuojami pagal formulę:

Z=U/I arba Z = R + J* (X_L -X_C)

Kur: Z – varža; R – aktyvi apkrova; X_L , X_C – indukcinė ir talpinė apkrova; J - koeficientas.

Nuoseklus ir lygiagretus elementų sujungimas

Elektros grandinės elementams (schemos atkarpai) būdingas taškas yra nuoseklusis arba lygiagretusis ryšys.

Atitinkamai, kiekvieną jungties tipą lydi skirtingas srovės srauto ir įtampos tiekimo modelis.Šiuo atžvilgiu Ohmo įstatymas taip pat taikomas skirtingai, atsižvelgiant į elementų įtraukimo variantą.

Serijiniu būdu sujungtų varžinių elementų grandinė

Kalbant apie nuoseklųjį ryšį (grandinės dalis su dviem komponentais), naudojama tokia formuluotė:

• aš = aš₁ = aš₂ ;
• U = U₁ +U₂ ;
• R = R₁ + R₂

Ši formuluotė aiškiai parodo, kad nepaisant nuosekliai sujungtų varžinių komponentų skaičiaus, srovės, tekančios per grandinės atkarpą, vertė nesikeičia.

Varžinių elementų sujungimas grandinės atkarpoje nuosekliai vienas su kitu. Ši parinktis turi savo skaičiavimo įstatymą. Diagramoje: I, I1, I2 - srovės srautas; R1, R2 - varžiniai elementai; U, U1, U2 - taikoma įtampa

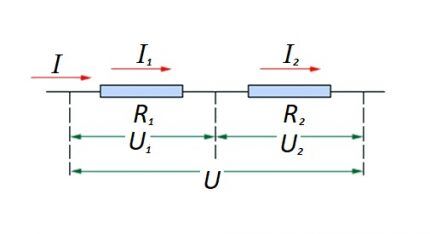
Įtampos, taikomos efektyviosioms varžinėms grandinės sudedamosioms dalims, dydis yra suma ir bendra EMF šaltinio vertė.

Šiuo atveju kiekvieno atskiro komponento įtampa yra lygi: Ux = I * Rx.

Bendra varža turėtų būti laikoma visų grandinės varžinių komponentų verčių suma.

Lygiagrečiai sujungtų varžinių elementų grandinė

Tuo atveju, kai yra lygiagretus varžinių komponentų ryšys, ši formuluotė laikoma teisinga, atsižvelgiant į vokiečių fiziko Ohmo įstatymą:

• aš = aš₁ +I₂ … ;
• U = U₁ = U₂ … ;
• 1/R = 1/R₁ + 1/R₂ + …

Neatmetama galimybė sukurti „mišraus“ tipo grandinės dalis, kai naudojamos lygiagrečios ir nuoseklios jungtys.

Varžinių elementų sujungimas grandinės atkarpoje lygiagrečiai vienas kitam. Šiam variantui taikomas kitoks skaičiavimo įstatymas. Diagramoje: I, I1, I2 - srovės srautas; R1, R2 - varžiniai elementai; U yra tiekiama įtampa; A, B – įėjimo/išėjimo taškai

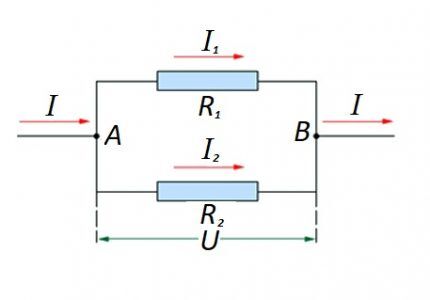
Tokiems variantams skaičiavimas paprastai atliekamas iš pradžių apskaičiuojant lygiagrečiojo jungties varžą. Tada prie gauto rezultato pridedama nuosekliai sujungto rezistoriaus vertė.

Integralios ir diferencinės teisės formos

Visi aukščiau išvardinti taškai su skaičiavimais taikomi sąlygomis, kai elektros grandinėse naudojami, taip sakant, „homogeniškos“ struktūros laidininkai.

Tuo tarpu praktikoje dažnai tenka susidurti su schemų konstravimu, kai skirtingose ​​atkarpose keičiasi laidininkų struktūra. Pavyzdžiui, naudojami didesnio skerspjūvio arba, atvirkščiai, mažesni, pagaminti iš skirtingų medžiagų.

Siekiant atsižvelgti į tokius skirtumus, yra vadinamasis „diferencialinis-integralus Ohmo įstatymas“. Be galo mažam laidininkui srovės tankio lygis apskaičiuojamas priklausomai nuo įtampos ir laidumo vertės.

Skirtumui apskaičiuoti naudojama ši formulė: J = ό * E

Atitinkamai integraliniam skaičiavimui formulė yra tokia: I * R = φ1 – φ2 + έ

Tačiau šie pavyzdžiai yra artimesni aukštosios matematikos mokyklai ir iš tikrųjų nėra naudojami tikroje paprasto elektriko praktikoje.

Išvados ir naudingas vaizdo įrašas šia tema

Išsami Ohmo dėsnio analizė žemiau esančiame vaizdo įraše padės pagaliau įtvirtinti žinias šia kryptimi.

Unikali vaizdo pamoka kokybiškai sustiprina teorinį rašytinį pristatymą:

Elektriko darbas ar elektronikos inžinieriaus veikla yra neatsiejama nuo momentų, kai iš tikrųjų reikia laikytis Georgo Ohmo dėsnio. Tai yra tam tikros tikrovės, kurias turėtų žinoti kiekvienas specialistas.

Didelių žinių šiuo klausimu nereikia – pakanka išmokti tris pagrindinius formuluotės variantus, kad būtų sėkmingai pritaikyta praktikoje.

Ar norėtumėte papildyti aukščiau pateiktą medžiagą vertingais komentarais ar išreikšti savo nuomonę? Rašykite komentarus bloke po straipsniu. Jei turite klausimų, nedvejodami kreipkitės į mūsų ekspertus.